|
(40)
|
Клетки различных органов могут быть подразделены на два типа: возбудимые клетки нервных волокон, сердца, клетки гладкой и скелетной мускулатуры, и невозбудимые клетки, к которым относятся, в частности, клетки эпителия и фоторецепторы. После приложения электрического тока невозбудимые клетки сразу релаксируют к своему первоначальному состоянию. В возбудимых клетках возникает последовательность процессов, зависящая от величины импульса пропускаемого через мембрану тока. Если импульс имеет надпороговую величину, на возбудимой мембране нервного волокна возникает одиночный нервный импульс - потенциал действия - который длится примерно 1 мс и распространяется по нервному волокну со скоростью от 1 до 100 м/с, сохраняя постоянную амплитуду и форму.
Современные представления о генерации нервного импульса основаны на работах
А. Ходжкина, А. Хаксли и Б. Катца, выполненных на гигантских
нервных волокнах кальмара (1952) и удостоенных нобелевской премии.
Механизм распространения электрического импульса вдоль мембраны аксона (толщина
около 50-70 Ангстрем) связан с тем, что проницаемость мембраны зависит от
имеющихся токов и напряжений, и различна для разного сорта ионов. Главную роль в
процессе играют ионы натрия (Na+ и K+). Важную роль в
регуляции процессов играют также ионы кальция. Первая модель распространения
электрического импульса вдоль аксона гигантского кальмара была предложена Ходжкиным и Хаксли (1952), и до сих пор является базовой
моделью для описания такого типа явлений. Рассматривается положительно
направленный ток (I) от внутренней к внешней стороне
мембраны аксона. Ток I(t) состоит из потоков ионов через
мембрану и тока, вызванного изменением трансмембранного потенциала на мембране,
обладающей емкостью C. Общее уравнение для изменения
тока:
Здесь C - емкость мембраны, Ii - вклад токов за счет трансмембранного переноса
ионов. На основании экспериментальных данных, Ходжкин и Хаксли записали
следующее выражение для Ii:
где V - потенциал, INa, IK, IL - соответственно натриевый, калиевый токи и ток
"утечки", обусловленный токами других ионов через мембрану, g - величины проводимости мембраны для соответствующих типов
ионов, V - равновесные потенциалы. Величины m, n,h -
переменные, изменяющиеся от 0 до 1, для которых справедливы полученные
эмпирически дифференциальные уравнения:
Качественно anam(1 + tan hV)/2, а ah(1 - tan hV)/2.
Если к мембране приложен импульс тока Ia(t), уравнение (40)
принимает вид:
Cовокупность уравнений (40-43)
и составляет систему из четырех уравнений, известную как система Ходжкина-Хаксли (1952). Она рассчитывается численно и
хорошо воспроизводит наблюдаемые в эксперименте явления протекания натриевого и
калиевого тока через мембрану аксона кальмара. Система имеет стабильное стационарное
состояние в отсутствие внешних токов, но когда приложенный импульс тока выше
порогового значения, демонстрирует регулярное периодическое возбуждение
мембраны.
Модель удается упростить в соответствии с временной иерархией переменных
m, n, h.
Натриевые токи (величина m) протекают гораздо быстрее,
чем калиевые (величина n), поэтому в соответствии с теоремой Тихонова можно заменить дифференциальные уравнения
для натриевой составляющей на алгебраические (dm/dt=0).
Если считать, что токи утечки протекают еще более медленно (h =
h0 = const), модель сводится к системе уравнений для двух
переменных
где 0 < a < 1, b и g - положительные константы, v играет роль потенциала V, а w - характеризует нелинейные свойства проводимости мембраны для
всех типов ионов. Модель Фитцхью-Нагумо (44)
(FitzHugh 1961, Nagumo et al. 1962) хорошо аналитически
исследована и часто используется в качестве локального элемента при описании
распространения волн в активных биологических средах, таких как сердечная мышца
(рис.
16), или мозговая ткань.
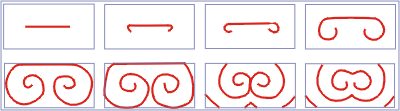 |
Рис. 15. Эволюция спиральной волны
в модели Фитц–Хью-Нагумо (
|
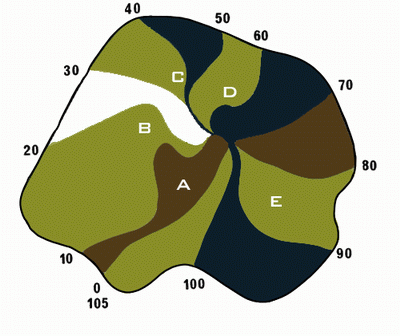 |
Рис. 16. Спиральные волны
распространения потенциала в сердце кролика (эксперимент |
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ