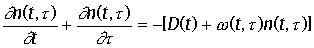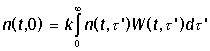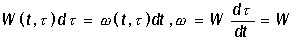Динамические модели в биологии

Непрерывные модели оперируют не с численностями отдельных групп, а с непрерывной функцией распределения организмов по возрастам. Уравнение для плотности функции распределения было впервые получено Мак-Кендриком в 1926 г., а затем "переоткрыто" фон Ферстером в 1959 г. и носит его имя. Это уравнение представляет собой дифференциальную форму закона сохранения числа особей. В уравнении две независимые переменные - время t и возраст t, который отсчитывается с момента рождения особи. n(t, t) dt - количество особей, имеющих возраст в интервале [t,t+dt]. Общее число особей всех возрастов в момент времени t определяется интегралом

. Уравнение Ферстера имеет вид:

(24)

В уравнении (24) слева стоит полная производная dn / dt, при этом учтено, что dt / dt = 1, в правой части уравнения - члены, которые описывают процессы, приводящие к изменению числа клеток данного возраста. Убыль клеток может быть вызвана разными причинами - смертностью, миграцией, для проточной культуры всеми этими процессами можно пренебречь по сравнению с протоком клеток через культиватор. Скорость протока D(t) не зависит от возраста клеток, но может зависеть от времени. Член

-w(t, 
t) u(t, t)

описывает убыль клеток из данного интервала возрастов при делении на дочерние со скоростью w. Прирост численности в результате размножения происходит в нулевой возраст и войдет в граничное условие при t = 0.

(25)

Здесь k - число потомков в одном акте размножения, W(t, t') dt' - вероятность размножения родителя в возрастном интервале [t', t' + dt'], равная удельной скорости размножения;

(26)

Если родители остаются в популяции после размножения (дрожжи), то W(t, t) - плотность безусловной вероятности деления в возрасте t (функция распределения возрастов деления). Если же клетки выбывают из своей возрастной группы после деления (водоросли, бактерии), то W(t, t) - плотность условной вероятности разделиться в возрасте t, если клетка дожила до этого возраста, не разделившись.

Имеются модели, описывающие распределение клеток по размерам и массам. Их легче сопоставлять с экспериментальными данными, так как имеются экспериментальные методы определения размеров клеток. Активно разрабатываются методы микроизмерений, позволяющие определить и другие параметры отдельных клеток (например, фотосинтетическую активность, содержание хлорофилла в водорослях, внутриклеточное рН и др.). Все большее распространение получают методы проточной микрофлуорометрии, позволяющие регистрировать спектральные характеристики сотен и тысяч микроорганизмов и строить соответствующие распределения признаков отдельных особей. Информация об эволюции этих распределений дает новые возможности оценки состояния популяций микроорганизмов, например, состояний популяций планктона в морях, почвенных микроорганизмов, клеток крови.

Динамические модели в биологии

Реестр моделей

Динамика популяций

Непрерывные модели возрастной структуры