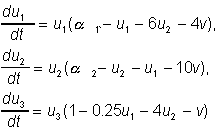 (24)
(24) Динамика сообществ, состоящих из многих видов или внутривидовых групп, не может быть исследована аналитически. Тем более усложняется задача при учете запаздывания или случайных факторов. Уже для системы из трех видов в случае разветвленной трофической цепи даже исследование автономной локальной системы становится чрезвычайно сложным по двум причинам.
Во-первых, качественная теория дифференциальных уравнений, служащая действенным инструментом для исследования систем второго порядка, не столь хорошо разработана для систем третьего и более высокого порядка. В значительной степени остается открытым вопрос о структуре и классификации притягивающих объектов аттракторов (стационарных режимов) в фазовых пространствах выше трех. Во-вторых , системы дифференциальных уравнений, описывающих динамику трех и более видов или внутривидовых групп, даже после нормировки содержат большое число параметров.
В последние годы в качественной теории дифференциальных уравнений получены принципиально новые результаты (Лоренц, Арнольд, Синай), показывающие существование в системах дифференциальных уравнений третьего и более высокого порядка наряду с точками равновесия (стационарными состояниями) и предельными циклами (регулярными колебаниями) притягивающих режимов типа так называемых "странных аттракторов". Эти режимы представляют собой области в фазовом пространстве, плотно заполненные фазовыми траекториями. Такие режимы соответствуют квазистохастической динамике, когда численность популяции не может быть точно предсказана, а можно говорить лишь о статистических характеристиках популяционной кривой.
В таких областях квазистохастического поведения малые начальные отклонения фазовых переменных приводят к экспоненциально быстрому разбеганию траекторий. Примером системы, обладающей различными типами поведения в зависимости от соотношения параметров, в том числе демострирующей динамический хаос, является рассмотренная А.Д. Базыкиным с сотр. модель хищник - две жертвы:
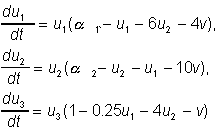
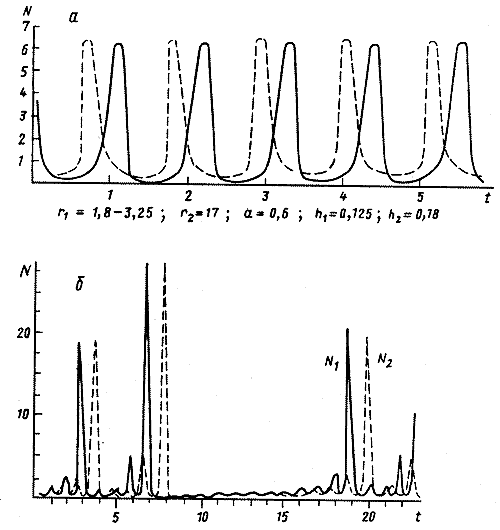 Рис.11. Модель популяции насекомых с активными стадиями имаго (кривая 1) и личинок (кривая 2). а. Колебания численностей. б. Вспышки численности. (Колесов, 1982) |
Здесь u1, u2 - безразмерные численности жертв, v - безразмерная численность хищников, 1, 2, - параметры, соответствующие скоростям роста численностей жертв. В системе наряду с устойчивым состояния равновесия возможны колебательные изменения численностей всех трех видов. В некоторой области параметров в системе имеется предельный цикл сложной формы. При уменьшении 2, наблюдается серия последовательных удвоений цикла (рис. 11 (а-в)).
В некотором диапазоне значений 2, из результатов численного эксперимента видно, что траектория системы полностью заполняет некоторый фазовый объем. При этих значениях параметров поведение системы неотличимо от случайного, т.е. является квазистахостическим (рис. 11г). Модельному режиму, изображенному на рис. 11г соответствуют наблюдаемые в природе нерегулярные изменения численностей животных.
Модели природных сообществ, где сосуществуют несколько видов, каждый из которых может быть подразделен на ряд половых и возрастных групп, обычно представляют собой системы из десятков уравнений и не поддаются аналитическому исследованию. Особенно сложную динамику имеют популяции высших животных. Так в работах Фрисмана при моделировании динамики численности морского котика с целью оптимизации промысла популяция делилась на 20 возрастных и половых групп. Прогнозирование поведения таких систем , несмотря на возможности вычислительной техники, представляет плохо формализованную задачу. Иногда удается упростить систему, сделать ее "прозрачной" для интерпретации, но, как правило, приходится сталкиваться с трудностями как в понимании закономерностей, лежащих в основе взаимодействия как видов и внутривидовых групп, так и в определении входящих в модель параметров.
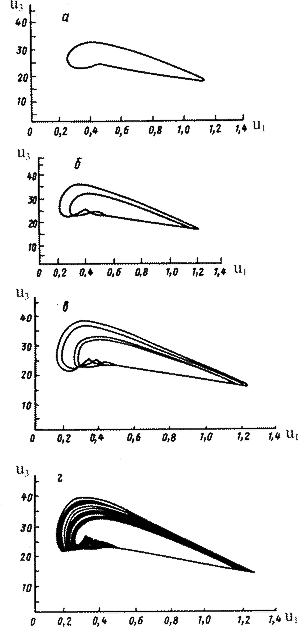 Рис.12. Система трех взаимодействующих видов: хищник - две жертвы (А.Д.Базыкин, 1985). Усложнение траектории (последовательное удвоение предельного цикла) при уменьшении параметра скорости роста первой жертвы. а - г. Колебательная динамика переходит в квазистохастическую. |
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ