Данная и последующие части работы посвящены рассмотрению наиболее важных теоретических положений и некоторых перспективных численных методов решения задач для параболических уравнений второго порядка с несамосопряженными операторами - задач конвекции (адвекции) – диффузии или, в более общей постановке, задач конвекции (адвекции) – диффузии - реакции. При этом мы будем пока ориентироваться, главным образом, на решение задачи моделирования пространственно-временной динамики нестратифицированных водных экосистем (методы численного решения трехмерных задач требуют отдельного рассмотрения). Мы не ставили перед собой цель дать полный обзор литературы по этому вопросу. Будут рассмотрены, в основном, только те алгоритмы, которые всесторонне исследованы теоретически, и, кроме того, успешно применялись для решения реальных (а не только тестовых) задач механики сплошной среды, при моделировании водных экосистем, изучении распространения консервативных и неконсервативных примесей в атмосфере и водной среде.
В целом, теория разностных методов решения задач математической физики применительно к проблемам окружающей среды развивается в следующих основных направлениях (Белов и др., 1989; Марчук, 1980; Марчук, 1988; Марчук, Саркисян, 1988; Мезингер, Аракава, 1979; Пененко, 1981; Самарский, Вабищевич, 1999; Arakawa, 1997; McRae et al., 1982):
·построение дискретных аналогов, аппроксимирующих исходную дифференциальную задачу и наследующих основные ее свойства;
·исследование устойчивости (корректности) разностной задачи;
·способы эффективной и экономичной численной реализации;
·способы фильтрации значений переменных, которые не соответствуют смыслу решаемой задачи (например, отрицательных температур воды или отрицательных концентраций веществ);
·способы предотвращения и подавления вычислительной неустойчивости при интегрировании систем уравнений на длительный срок.
Выбор той или иной формы дифференциального уравнения и его дискретного аналога не всегда очевиден и диктуется некоторыми дополнительными соображениями как физического, так и вычислительного характера. Поэтому естественно рассмотреть и проанализировать различные формы уравнения конвекции (адвекции) - диффузии, отметив их основные особенности. Можно выделить три основных класса таких задач, которые связаны с дивергентной, недивергентной и симметричной формой записи операторов конвективного переноса (Самарский, Вабищевич, 1999). В том случае, когда используется дивергентная форма уравнения конвекции - диффузии, неизвестная функция ![]() определяется из уравнения
определяется из уравнения
![]() . (1)
. (1)
В дивергентной (консервативной) форме уравнение конвекции - диффузии явно выражает соответствующий закон сохранения. В некоторых случаях лучше записывать уравнение конвекции - диффузии в недивергентной форме. Тогда неизвестная функция ![]() определяется из уравнения
определяется из уравнения
![]() . (2)
. (2)
Уравнение с недивергентными конвективными слагаемыми является основным при рассмотрении краевых задач для параболических уравнений второго порядка. Заслуживает специального выделения и так называемая симметричная форма уравнения конвекции - диффузии. В этом случае конвективный перенос представляется в виде полусуммы конвективного переноса в дивергентной и недивергентной формах, то есть в виде
![]() . (3)
. (3)
Как правило, рассматриваются только линейные уравнения конвекции - диффузии. Типичной является зависимость коэффициента диффузии от точки пространства (неоднородные среды), коэффициента конвективного переноса (скорости) не только от точки пространства, но и от времени, то есть ![]() ,
, ![]() ,
, ![]() .
.
В случае двумерной задачи, на решение которой мы и будем ориентироваться, нестационарное уравнение конвекции - диффузии с конвективными слагаемыми в недивергентном виде можно записать следующим образом
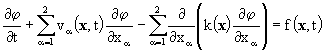 . (4)
. (4)
Это уравнение дополняется соответствующими начальными и граничными условиями. Вторым примером является нестационарное уравнение конвекции - диффузии с конвективным переносом в дивергентной форме:
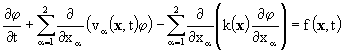 . (5)
. (5)
Уравнение конвекции - диффузии с конвективными слагаемыми в симметричной форме записывается в следующем виде
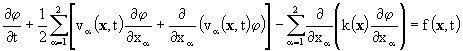 . (6)
. (6)
Введем в рассмотрение операторы диффузионного и конвективного переноса. Оператор диффузионного переноса D определяется выражением
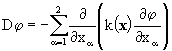 . (7)
. (7)
Оператор конвективного переноса в соответствии с (4) - (6) записывается в различных формах. Так, для оператора конвективного переноса в недивергентной форме в соответствии с (4) положим ![]() , где
, где
![]() . (8)
. (8)
Для оператора конвективного переноса в дивергентной форме в соответствии с (5) положим ![]() , где
, где
![]() . (9)
. (9)
С учетом (6) оператор конвективного переноса в симметричной форме имеет вид ![]() , таким образом
, таким образом
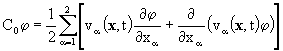 . (10)
. (10)
С учетом соотношений (7) - (10), нестационарную задачу конвекции - диффузии можно записать в виде дифференциально-операторного уравнения
![]() в
в ![]() ,
, ![]() , (11)
, (11)
где ![]() ,
, ![]() на
на ![]() ,
, ![]() в
в ![]() при t = 0.
при t = 0.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ