Пусть в задаче (1.1) - (1.2) оператор А зависит от времени и его можно представить в виде суммы положительно полуопределенных матриц: 
, 
, 
, имеющих достаточно гладкие по t элементы. Рассмотрим аппроксимации этих матриц на временном интервале 
в форме 
. Схема покомпонентного расщепления для однородной задачи (1.1) - (1.2) имеет вид
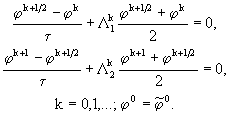(17)
Эту систему разностных уравнений без вспомогательных функций 
на промежуточном временном слое 
можно привести к одному операторному уравнению
, (18)
где
. (19)
Пусть выполнено условие
, (20)
Тогда схема (17) абсолютно устойчива. Она обладает вторым порядком аппроксимации по 
, если 
и 
коммутируют и первым, если 
и 
не коммутируют. Действительно, разложим оператор 
по степеням 
: 
. Если операторы 
коммутируют, то есть 
, то разложение 
можно записать в виде 
. Тогда уравнение (18) запишется в виде
(21)
или
. (22)
Подставляя в последнее равенство выражение 
из (21), имеем
.
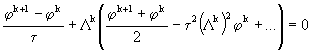Сравнивая эту схему со схемой Кранка - Николсона (8), заключаем, что порядок аппроксимации схемы (17) отличается от порядка аппроксимации схемы (8) на величину 
. Следовательно, в случае 
схема (17) обладает вторым порядком аппроксимации по 
, если же 
, схема (17) обладает только первым порядком аппроксимации. Абсолютная устойчивость схемы (17) следует из неравенства
и оценок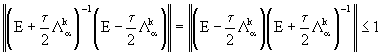 
, вытекающих их леммы Келлога.
Схема (17) реализуется следующим образом:
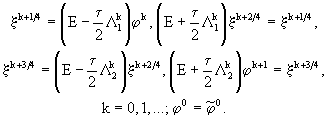(23)
Если разбиение исходного оператора А на сумму двух операторов осуществлено так, что возможно эффективное решение уравнений с матрицами 
, то и реализация всего алгоритма будет эффективной.
Дополнительная информация:
© 2001-2026 Кафедра биофизики МГУ