Следующий класс методов расщепления - метод предиктор-корректор (или схема аппроксимационной поправки) (Марчук, 1988). Эти методы мы также рассмотрим в применении к матричным эволюционным уравнениям типа (1.1) - (1.2) и (3.1) - (3.2) с оператором, не зависящим от времени.
Общая идея метода предиктор-корректор состоит в следующем. Весь интервал 
разбивается на частичные промежутки и в пределах каждого из элементарных промежутков 
задача (1.1) - (1.2) или (3.1) - (3.2) решается в два приема. Сначала по схеме первого порядка точности с довольно значительным "запасом" устойчивости находится приближенное решение задачи на момент времени 
. Этот этап обычно называется предиктором. После этого на всем интервале 
расписывается исходное уравнение со вторым порядком аппроксимации, которое служит корректором. Существенно именно то, что при построении корректора используется "грубое" решение, найденное с помощью предиктора на момент времени 
.
Схема предиктор-корректор для однородной задачи (1.1) - (1.2) может быть записана в следующей форме:
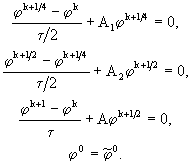(49.1)
Если из первых двух уравнений системы (49.1) исключить вспомогательную функцию 
, то получим
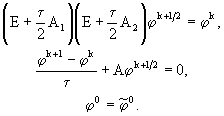(49.2)
Исключая из этих уравнений 
, получим
. (49.3)
Пусть, далее, выполнено ограничение 
. Если 
и элементы операторов не зависят от времени, то при достаточной гладкости решения 
задачи (1.1) - (1.2) разностная схема (49.1) является абсолютно устойчивой и аппроксимирует исходную задачу со вторым порядком точности по 
. В самом деле, (49.3) с помощью алгебраических преобразований приводится к виду
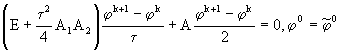. (49.4)
Нетрудно заметить, что это разностное уравнение при достаточной гладкости решения по порядку аппроксимации совпадает со схемой Кранка - Николсона (8)
, 
,
то есть имеет второй порядок аппроксимации по 
. Для разностной схемы (49.1) справедлива оценка
, (50)
где 
, 
. Исследуем устойчивость этого метода. С этой целью уравнение (49.3) запишем в виде
(51)
где
. (52)
Разностное уравнение (51) устойчиво, так как
, (53)
а 
, 
. Отсюда, с учетом соотношений (52) и (53), получим: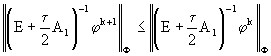 
, или 
, что и обеспечивает устойчивость схемы. Отметим также , что хотя разностная схема (49.1) абсолютно устойчива, но входящая в нее как часть разностная схема для корректора, рассмотренная отдельно, может быть абсолютно неустойчивой. Однако тот запас устойчивости, которым обладает предиктор, достаточен для абсолютной устойчивости схемы в целом.
Для неоднородной задачи метод предиктор - корректор сформулируем следующим образом:
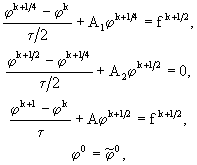(54.1)
где 
. При таком выборе 
(54.1) аппроксимирует исходную задачу со вторым порядком по 
. Устойчивость схемы (54.1) устанавливается следующим образом. Последовательно исключая 
и 
, получим
. (54.2)
Введем обозначение 
. Тогда соотношение (54.2) приводится к виду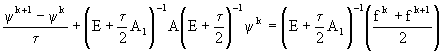 
. Разрешая это уравнение относительно 
, получим
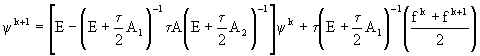. (54.3)
Поскольку имеет место соотношение
,
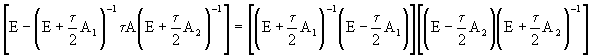то согласно лемме Келлога и соотношению 
получаем оценку
, (55)
где 
, то есть при 
снова имеем устойчивость разностной схемы. Таким образом, если 
, 
и элементы матриц 
, 
не зависят от времени, то при достаточной гладкости решения и правой части f задачи разностная схема (54.1) абсолютно устойчива и позволяет получать решения второго порядка точности по 
.
Дополнительная информация:
© 2001-2024 Кафедра биофизики МГУ