Ограниченный рост. Уравнение Ферхюльста

Базовой моделью, описывающей ограниченный рост, является модель Ферхюльста (1848):

(2)

Параметр K носит название "емкости популяции", выражается в единицах численности (или концентрации) и носит системный характер, то есть определяется целым рядом различных обстоятельств, среди них - ограничения на количество субстрата для микроорганизмов, доступного объема для популяции клеток ткани, пищевой базы или убежищ для высших животных. График зависимости правой части уравнения (2) от численности x и численности популяции от времени представлены на рис. 1 (а и б).

Рис. 1. Ограниченный рост. Зависимость величины скорости роста от численности (а) и численности от времени (б) для логистического уравнения.

Изучение дискретного аналога уравнения (2) во второй половине 20 века выявило совершенно новые и замечательные его свойства [Ризниченко Г. Ю., Рубин А. Б. Математические модели биологических продукционных процессов; Murray J. D. Mathematical Biology]. Рассмотрим численность популяции в последовательные моменты времени, что соответствует реальной процедуре пересчета особей (или клеток) в популяции. Зависимость численности на временном шаге номер n+1 от численности предыдущем шаге n можно записать в виде:

x_n+1 = rx_n (1 - x_n) (3)

Поведение во времени переменной x_n в зависимости от величины параметра r может носить характер не только ограниченного роста, как было для непрерывной модели (2), но также быть колебательным или квазистохастическим, как это изображено на рис. 2 слева. Сверху вниз значение параметра собственной скорости роста r увеличивается. Кривые, представляющие вид зависимости значения численности в данный момент времени (t+1) от значений численности в предыдущий момент времени t представлены на рис. 2 слева, эта скорость нарастает при малых численностях, и убывает, а затем обращается в нуль при больших численностях. Динамический тип кривой роста популяции зависит от того, насколько быстро происходит рост при малых численностях, т.е. определяется производной (тангенсом угла наклона этой кривой) в нуле, который определяется коэффициентом r:

Для небольших r (r < 3) численность популяции стремится к устойчивому равновесию;
Когда график слева становится более крутым, устойчивое равновесие переходит в устойчивые циклы. По мере увеличения численности длина цикла растет, и значения численности повторяются через 2, 4, 8,..., 2n поколений;
При величине параметра r > 2,570 происходит хаотизация решений. При достаточно больших r динамика численности демонстрирует хаотические всплески (вспышки численности насекомых). Уравнения такого типа описывают динамику численности сезонно размножающихся насекомых с неперекрывающимися поколениями.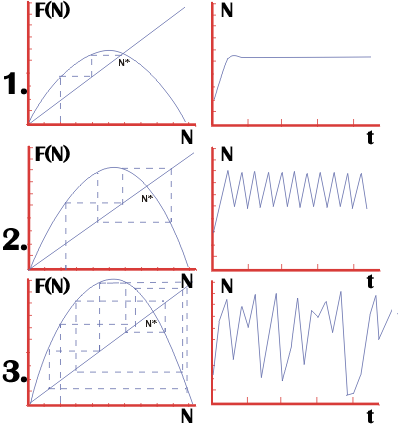

Рис. 2.

Вид 
      функции зависимости численности на последующем шаге от численности на 
      предыдущем шаге (а) и 
      поведение численности во времени (б) при разных значениях параметра r для дискретной модели логистического 
      роста (3): 
      1 – ограниченный рост; 
      2 – колебания; 3 – хаос.

Дискретное описание оказалось продуктивным для систем самой различной природы. Аппарат представления динамического поведения системы на плоскости в координатах [x_t, x_t+T] позволяет определить, является наблюдаемая система колебательной или квазистохастической. Например, представление данных электрокардиограммы позволило установить, что сокращения человеческого сердца в норме носят нерегулярный характер, а в период приступов стенокардии или в предынфарктном состоянии ритм сокращения сердца становится строго регулярным. Такое "ужесточение" режима является защитной реакцией организма в стрессовой ситуации и свидетельствует об угрозе жизни системы.

Дополнительная информация:

печатные издания и Интернет-сайты (38)

В начало

Динамические модели в биологии

Реестр моделей

Базовые модели математической биофизики

Ограниченный рост. Уравнение Ферхюльста