Динамические модели в биологии

Реестр моделей

Базовые модели математической биофизики

Классические модели Лотки и Вольтерра

Первое понимание, что собственные ритмы возможны в богатой энергией системе за счет специфики взаимодействия ее компонентов пришло после появления простейших нелинейных моделей взаимодействия химических веществ в уравнениях Лотки, и взаимодействия видов - в моделях Вольтерра [Вольтерра В. Математическая теория борьбы за существование; Ризниченко Г. Ю., Рубин А. Б. Математические модели биологических продукционных процессов]. Уравнение Лотки рассмотрено им в 1925 г. в книге «Элементы физико-химической биологии» и описывает систему следующих химических реакций:

A ® X Û Y ® B

В некотором объеме находится в избытке вещество A. Молекулы A с постоянной скоростью (константа k0) превращаются в молекулы вещества X (реакция нулевого порядка). Вещество X может превращаться в вещество Y, причем скорость этой реакции тем больше, чем больше концентрация вещества Y - реакция второго порядка. В схеме это отражено обратной стрелкой над символом ®. Молекулы Y в свою очередь необратимо распадаются, в результате образуется вещество B (реакция первого порядка). Систему уравнений, описывающих реакцию, имеет вид:

(9)

Здесь X, Y, B - концентрации химических компонентов. Первые два уравнения системы не зависят от B, поэтому их можно рассматривать отдельно. При определенных значениях параметров в системе возможны затухающие колебания.
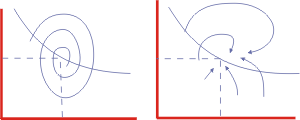Рис. 4. Модель химических реакций Лотки. Фазовый портрет системы при значениях параметров, соответствующих затухающим колебаниям.

Базовой моделью незатухающих колебаний является классическое уравнение Вольтерра, описывающее взаимодействие видов типа хищник-жертва. Как и в моделях конкуренции (8), взаимодействие видов описывается в соответствии с принципами химической кинетики: скорость убыли количества жертв (x) и скорость прибыли количества хищников (y) считается пропорциональными их произведению

dx / dt = ax – bxy,
dy / dt = cxy – dy 		(10)



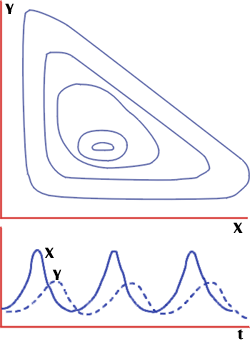Рис. 5. Модель хищник – жертва Вольтерра, описывающая незатухающие колебания численности: а – фазовый портрет; б – зависимость численности жертвы и хищника от времени

На рис. 5 представлены фазовый портрет системы, по осям которого отложены численности жертв (x) и хищников (y) - (а) и кинетика численности обоих видов - зависимость численности от времени - (б). Видно, что численности хищников и жертв колеблются в противофазе.Простейшая модель Вольтерра (10) имеет один существенный недостаток: параметры колебаний ее переменных меняются при флуктуациях параметров и переменных системы (негрубая система).

 

Дополнительная информация:

 

В начало

© 2001-2025 Кафедра биофизики МГУ